재귀 함수 (Recursion Function)
- 본인을 참조하는 함수
class Program
{
static void Main(string[] args)
{
Recur();
}
static void Recur()
{
// 함수 내부에서 본인을 다수 호출함
Recur();
}
}
재귀 함수는 아주 간단하게 설명하자면 함수안에서 다시 함수를 다시 호출 하는 것을 말함.
- 무한루프에 빠지지 않기 위한 종료 트리거
class Program
{
static void Main(string[] args)
{
Recur(10);
}
static void Recur(int end)
{
System.Console.WriteLine($"IDX : {end}");
// 종료 트리거
if (end == 0)
{
System.Console.WriteLine($"EXIT");
return;
}
// 본인을 다시 호출
Recur(end-1);
}
}
무한루프에 빠지지 않게 하기 위해 필수적으로 종료 트리거가 필요함.
- 재귀함수의 장/단점
class Program
{
static void Main(string[] args)
{
int sum = AddReCur(10);
System.Console.WriteLine(sum);
sum = AddNotRecur(10);
System.Console.WriteLine(sum);
}
// 재귀 함수로 num 부터 0 까지의 함 구하기
static int AddReCur(int num)
{
return num == 0 ? 0 : num + AddReCur(num - 1);
}
// 그냥 num 부터 0 까지의 합 구하기
static int AddNotRecur(int num)
{
int sum = 0;
for(int i = 0; i <= num; i++)
{
sum += i;
}
return sum;
}
}
장점은 직관적인 코드 표현과 간결함? 그런데 사실 잘 모르겠음.
단점은 메모리를 많이 소모 하고, 재수없으면 오퍼플로어 발생함.
솔직히 그냥 FOR 문 쓰는게 나은거 같음. 이건 그냥 내생각임.
꼬리 재귀 함수 (Tail Recursion Function)
- 재귀 함수 VS 꼬리 재귀 함수 차이
class Program
{
static void Main(string[] args)
{
// 꼬리 재귀 함수 호출
int sum = AddTailRecur(5);
System.Console.WriteLine(sum);
// 재귀 함수 호출
sum = AddRecur(5);
System.Console.WriteLine(sum);
}
// 재귀 함수로 num 부터 0 까지의 함 구하기
static int AddRecur(int num)
{
if (num == 0)
return 0;
return num + AddRecur(num - 1);
}
// 꼬리 재귀 함수로 num 부터 0 까지의 합 구하기
static int AddTailRecur(int num, int sum = 0)
{
if (num == 0)
return sum;
return AddTailRecur(num - 1, sum + num);
}
}
재귀함수의 흐름
AddRecur(5)
{
5 + AddRecur(5 -1)
{
4 + AddRecur(4 -1)
{
3 + AddRecur(3 - 1)
{
2 + AddRecur(2 - 1)
{
1 + AddRecur(1 - 1)
{
0
}
}
}
}
}
}
결국 아래와 같이 됨.
return 5 + return 4 + return 3 + return 2 + return 1 + return 0
return 5 + return 4 + return 3 + return 2 + return 1 + 0
return 5 + return 4 + return 3 + return 2 + 1
return 5 + return 4 + return 3 + 3
return 5 + return 4 + 6
return 5 + 10
꼬리재귀함수의 흐름
AddTailRecur(5, 0)
{
AddTailRecur(5 - 1, 0 + 5)
{
AddTailRecur(4 - 1, 5 + 4)
{
AddTailRecur(3 - 1, 9 + 3)
{
AddTailRecur(2 - 1, 12 + 2)
{
AddTailRecur(1 - 1, 14 + 1)
{
15
}
}
}
}
}
}
결국 아래와 같이 됨.
return + return + return + return + return + return 15
return + return + return + return + return 15
return + return + return + return 15
return + return + return 15
return + return 15
return 15
- 재귀함수의 단점을 보완한 꼬리재귀 함수
꼬리 재귀 함수도 재귀 함수와 같은 단점을 가지고 있는 구조 이다. 그런데 어떻게 단점을 보완 하였을까?
답은, 계산의 시점과 컴파일러에 있다.
1. 처리 시점
우선 합을 구하는 시점을 보게 되면..
재귀 함수는 리턴이 이루어지면서 순차적으로 덧셈을 처리 한다.
하지만 꼬리 재귀 함수는 함수를 호출하는 시점에 계산을 끝내고 그 결과 값을 같이 넘긴다. 그래서 최초 리턴이 시작되는 시점에 이미 덧셈이 다 끝나 있다.
결론은, 꼬리 재귀 함수가 되기 위해서는 최초 리턴이 이루어지는 시점에 이미 계산이 끝나있어야 한다.
2. 컴파일러
꼬리 재귀 함수의 경우 컴파일러에 최적화 설정을 해놓으면 꼬리 재귀 함수를 컴파일을 거치면서 FOR 문으로 변환 해준다. 그래서 메모리 소모로 인한 오버플로어가 발생하지 않는다.
- C# 컴파일러 설정
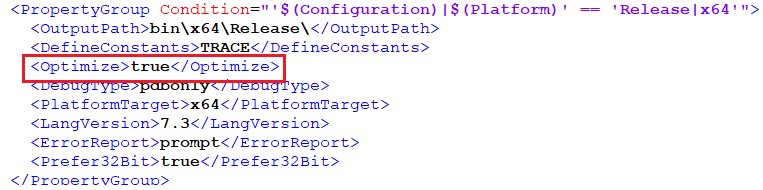
1. 프로젝트의 *.csproj 파일 열기.
2. 해당 프로퍼트 그룹의 항목 <Optimize>true</Optimize> 로 설정
'자료구조' 카테고리의 다른 글
| [자료구조] Graph (0) | 2021.09.09 |
|---|